数据挖掘算法
数据挖掘算法
分类
K-NN算法(k-Nearest Neighbors)
- 隶属于基于距离的分类算法,距离越近,相似性越大,反之相似性越小。
- 介绍:主要思想即计算每个训练数据到待分类元组的距离,取和待分类元组距离最近的k个训练数据,k个数据中占大多数的类别即待分类元组的所属类别。
- 作用范围:处理连续数据,应该注意需要数据集中每个特征都是连续数据,不允许特征出现离散数据。
- 具体操作
- 计算训练集中每个元组到待分类元组的距离,按距离从小到大的顺序选取最近距离的k个元组作为分类模型
- 使用投票法选取占比最多的类别即为待分类元组的类别
- 算法
1 | (1)N=\phi; |
决策树
- 介绍:决策树分类方法采取自顶向下的递归方式,从根节点到叶结点的一条路径就对应着一条合取规则。构造好的决策树关键在于如何选择好的逻辑判断或属性。研究表明,一般情况下,树越小则预测能力越强,所以要选择合适的产生分支的属性。由于构造最小树属于NP-难问题,因此只能采用启发式的策略来进行属性选择。属性选择依赖于对各种例子子集的不纯度度量方法,包括信息增益、信息增益比、距离度量、G统计、证据权重、MLP、相关度和Relief等。不同的度量有着不同的效果、特别是对于多值属性,选择合适的度量方法对于结果影响很大。
- 决策树生成算法:
1 | Generate_decision_tree(samples, attribute_list) /*决策树生成算法*/ |
- 决策树修剪:
基本的决策树构造算法没有考虑噪声,因此生成的决策树完全与训练例子拟合。在有噪声情况下,将导致过分拟合(Overfitting),即对训练数据的完全拟合反而使对现实数据的分类预测性能下降。现实世界的数据一般不可能是完美的,可能缺值(Missing Values);数据不完整;含有噪声甚至是错误的。剪枝是一种克服噪声的基本技术,同时它也能使树得到简化而变得更容易理解。剪枝过程中一般要涉及一些统计参数或阈值(如停机阈值)。要防止过分剪枝(Over-Pruning)带来的副作用。
ID3算法
介绍
ID3是Quinlan提出的一个著名决策树生成方法,决策树中每一个非叶结点对应着一个非类别属性,树枝代表这个属性的值。一个叶结点代表从树根到叶结点之间的路径对应的记录所属的类别属性值。
执行方式
- 训练数据集D,类别集合C={c1, c2, …, ck}
- 创建一个结点t,初始情况下训练数据集中的所有样本与根结点关联,记为Dt。将t设为当前结点。
- 如果当前结点t所关联的数据集Dt中所有样本的类别相同(假设为ci), 则将该结点标记为叶子节点,记录类别为ci,停止对该结点所关联的数据集的进一步分裂。接着处理其他非叶子节点。否则,进入下一步。
- 为数据集Dt选择分裂属性和分裂条件。根据分裂条件将数据集Dt分裂为m个子集,为结点t创建m个子女结点,将这m个数据集分别与之关联。依次将每个结点设为当前结点,转至步骤2进行处理,直至所有结点都标记为叶子结点。
步骤
- 从数据集中确定分类属性,求出分类属性的期望I
- 分别求出各个条件属性的熵E
-
- 设属性A具有个不同值{a1, a2, …, av} ,可以用属性A将样本S划分为 {S1, S2, …, Sv} ,设sij 是Sj中Ci类的样本数,则由A划分成子集的熵由上式给出
- 根据熵值与期望值,求得各个条件属性的信息增益值Gain
- 选取具有最大信息增益的条件属性作为分支节点
- 对新生成树的每个子表循环1-4步骤,直到分类器构建完成
C4.5算法
介绍
C4.5算法由ID3算法演变,在包含ID3算法功能外,新引入其它功能,如合并具有连续属性的值、可以处理具有缺少属性值的训练样本、K交叉验证等。由此C4.5算法可以处理离散属性数据,也可以处理连续属性数据。
合并具有连续值的属性
- 对连续值属性进行排序
- 针对排序后的连续数据进行划分,划分为两部分(比如连续属性A有n个取值,可以进行n次划分,保证划分的全面性)
- 针对每个划分分别计算增益比率,并进行比较,选择增益最大的划分来对相应的属性进行离散化处理
步骤
- 从数据集中确定分类属性,求出分类属性的期望I
- 分别求出各个条件属性的熵E
-
- 设属性A具有个不同值{a1, a2, …, av} ,可以用属性A将样本S划分为 {S1, S2, …, Sv} ,设sij 是Sj中Ci类的样本数,则由A划分成子集的熵由上式给出
- 根据熵值与期望值,求得各个条件属性的信息增益值Gain
- 求出各条件属性的SplitI
-
- 假如我们以属性A的值为基准对样本进行分割的话,Splitl(A)就是前面期望的信息值概念
- 由SpiltI与Gain,可以求得各个条件属性的信息增益比GainRatio
- 选取具有最大信息增益比的条件属性作为分支节点
- 对新生成树的每个子表循环1-6步骤,直到分类器构建完成
- 注意:在第七步时,由于产生了新的子表,子表数据集中分类属性的期望I值可能发生变化。同时,应注意,当条件属性为某一值如s1时,其产生的结果唯一(即分类属性对应的值确定唯一)该条件属性中s1的分支应当结束。
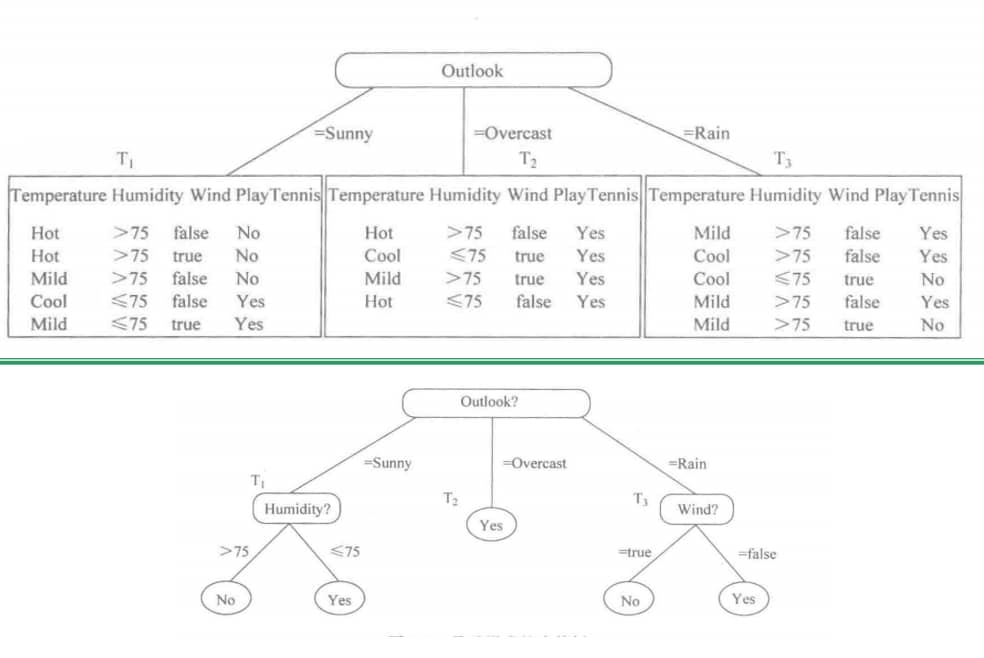
贝叶斯分类
介绍
贝叶斯分类是数据挖掘和机器学习中一类重要的概率分类方法,基于贝叶斯定理构建。常见的贝叶斯分类方法有朴素贝叶斯分类,贝叶斯网络,半朴素贝叶斯分类,贝叶斯最优分类等。贝叶斯分类的核心是贝叶斯定理
设X是类标号未知的数据样本。设H为某种假定,如数据样本X属于某特定的类C。对于分类问题,我们希望确定P(H|X),即给定观测数据样本X,假定H成立的概率。P(H)是先验概率,或称H的先验概率。P(X|H)代表假设H成立的情况下,观察到X的概率。P(H|X)是后验概率,或称条件X下H的后验概率。
朴素贝叶斯分类
条件
- 类条件独立性:即各个条件属性是相互独立的
原理
- 每个数据样本用一个n维特征向量X= {x1,x2,……,xn}表示,分别描述对n个属性A1,A2,……,An样本的n个度量。
- 假定有m个类C1,C2,…,Cm,给定一个未知的数据样本X(即没有类标号),分类器将预测X属于具有最高后验概率(条件X下)的类。也就是说,朴素贝叶斯分类将未知的样本分配给类Ci(1≤i≤m)当且仅当P(Ci|X)> P(Cj|X),对任意的j=1,2,…,m,j≠i。这样,最大化P(Ci|X)。其P(Ci|X)最大的类Ci称为最大后验假定。根据贝叶斯定理
- 由于P(X)对于所有类为常数,只需要P(X|Ci)*P(Ci)最大即可。如果Ci类的先验概率未知,则通常假定这些类是等概率的,即P(C1)=P(C2)=…=P(Cm),因此问题就转换为对P(X|Ci)的最大化(P(X|Ci)常被称为给定Ci时数据X的似然度,而使P(X|Ci)最大的假设Ci称为最大似然假设)。否则,需要最大化P(X|Ci)*P(Ci)。注意,类的先验概率可以用P(Ci)=si/s计算,其中si是类Ci中的训练样本数,而s是训练样本总数。
- 给定具有许多属性的数据集,计算P(X|Ci)的开销可能非常大。为降低计算P(X|Ci)的开销,可以做类条件独立的朴素假定。给定样本的类标号,假定属性值相互条件独立,即在属性间,不存在依赖关系。这样
- 对未知样本X分类,也就是对每个类Ci,计算P(X|Ci)*P(Ci)。样本X被指派到类Ci,当且仅当P(Ci|X)> P(Cj|X),1≤j≤m,j≠i,换言之,X被指派到其P(X|Ci)*P(Ci)最大的类。
公式
步骤
- 由下述公式可得正比于,由训练集求出
-
- P(X)由全概率公式可得在任何i下不变,所以成正比关系
- 根据贝叶斯定理,后验概率正比于似然与先验概率的乘积
- 在训练集内,通过求出
- 求出各条件属性的,累乘可求出
- 已知朴素贝叶斯的类条件独立性,由条件独立性假设我们可以得出如下公式
-
- 循环1,2步骤,求出分类属性可能对应的所有与
- 将该待分类项分到值大的部分,即
- 由可知,越大,越大
离散情况
- 在第3步骤中,求训练集中某条件属性在情况下出现的概率,若该属性 为离散属性,直接从训练集中提取的情况数据集,在数据集中计算的概率
连续情况
- 在第3步骤中,求训练集中某条件属性在情况下出现的概率,若该属性为连续属性,则通常假定该属性服从高斯分布,计算公式如下。其中为高斯分布函数,为均值与标准差
分类的补充问题
分类数据预处理
- 目前普遍认为不存在某种方法适用于各种特点的数据,同时分类的效果也与数据的特点有关。因此,在分类前应该对数据进行预处理。下面我们介绍数据清理,特征选择和数据变换三个预处理方式,分别解决不同的问题。
数据清理
- 目的:主要是消除或减少数据噪声和处理空缺值。
- 噪声处理:噪声是测量变量中的随机错误或偏差,可以使用数据平滑技术消除噪声。
- 举例:
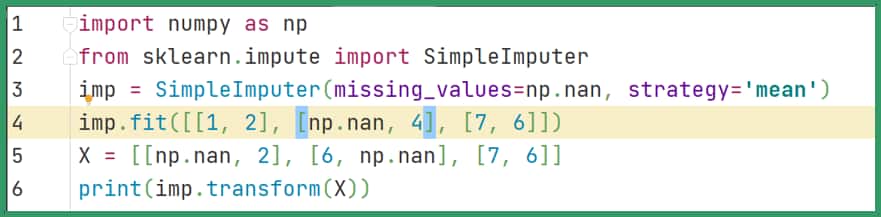
结果:[[4.,2.],[6.,4.],[7.,6.]]
解析:可用均值填补,先解决训练数据中的缺省问题,,即用其它两个没有缺省的元素求,求出第一个元素均值为4。由于第二个元素训练数据没有缺省,所以三个数据应该全部用上,即。用这两个均值分别填补下面数据的缺省值。
特征选择
- 概念:特征选择是指,从已知的一组特征集中按照某一准则选择出有很好的区分特性的特征子集,或按照某一准则对特征的分类性能进行排序,用于分类器的优化设计。
- 原因:数据中有很多属性可能与分类任务并无关系,这些属性可能会减慢或误导学习步骤,所以我们要去筛选特征
- 举例:这里我们以0-1伯努利分布为例,对于这种分布,我们可以采用设置方差阈值,删除低方差的特征值,因为低方差意味着在均值上下浮动较小,不影响分类。
1 | from sklearn.feature_selection import VarianceThreshold |
结果:阈值给定threshold=0.2244,利用伯努利随机变量的方差公式:方差 = p * (1 - p),分别求出每个特征的方差,低于阈值的直接删除,输出结果如下:
1 | [[1] |
数据变换
- 目的:通过平滑、聚集、数据概化、规范化、特征构造等手段将数据转换为适合于挖掘的形式。
- 名词介绍:
- 平滑:去掉数据中的噪声。
- 聚集:对数据进行汇总和聚集;例如可以聚集日销售数据,进而得到年和月的销售数据。
- 数据概化:用高层次的概念替换低层次的“原始”数据。例如Age可以映射到“青年、中年、老年”等。
- 规范化:将属性数据按比例缩放,使之落入一个特定的区间。
- 特征构造:构造新的属性值,帮助数据挖掘过程
规范化
- 目的:规范化特征值,将特征值放在同一量纲下,让模型公平对待每个特征。同时加速模型收敛,提高模型精度。
- 常用的规范方法:
- 标准化(Z-score标准化):
分类器性能的表示与评估
- 必要性:分类器性能是评价分类算法的重要因素,对于不同的数据,不同的分类算法将产生不同的分类结果。不同于传统算法对时间复杂度和空间复杂度的硬性要求,分类器的性能通常用准确率来评价。
- 分类器性能的表示方法类似信息检索系统的评价方法,可以采用OC曲线和ROC曲线、混淆矩阵
- 方法:混淆矩阵
给定一个类Cj和一个数据库元组ti,ti可能被分类器判定为属于Cj或不属于Cj,其实ti本身可能属于Cj或不属于Cj,这样就会产生如下一些情况:- 真正(True Positive): 预测为阳性(Positive),且真实值也是阳性。
- 假正(False Positive): 预测为阳性,但真实为阴性(假阳性)(表现为误报)。
- 真负(True Negative): 预测为阴性,且真实为阴性(正确拒绝)。
- 假负(False Negative): 预测为阴性,但真实为阳性(假阴性)(表现为漏报)。
注意:'真’指的是预测正确,即模型的预测值(Prediction)和真实值(Ground Truth)一致。'假’指的是二者不一致,即预测错误。
- TP,TF,FP,FN分别为以下情况:
- TP:11 (P为1,T表示预测一致,所以真实值也为1)
- TN:00 (N为0,T表示预测正确,所以实际值也为0)
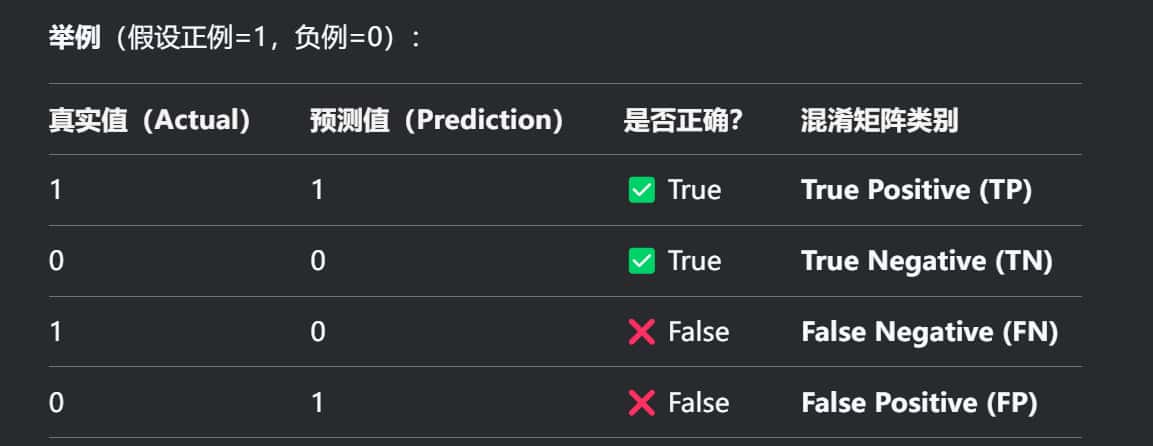
一般来说,没有指明"正例"的应该赋值,我们默认"正例"为1*(在0、1中)*
- 一般来说,对于混淆矩阵,我们默认矩阵的’行’为’实际值’,‘列’为’预测值’。
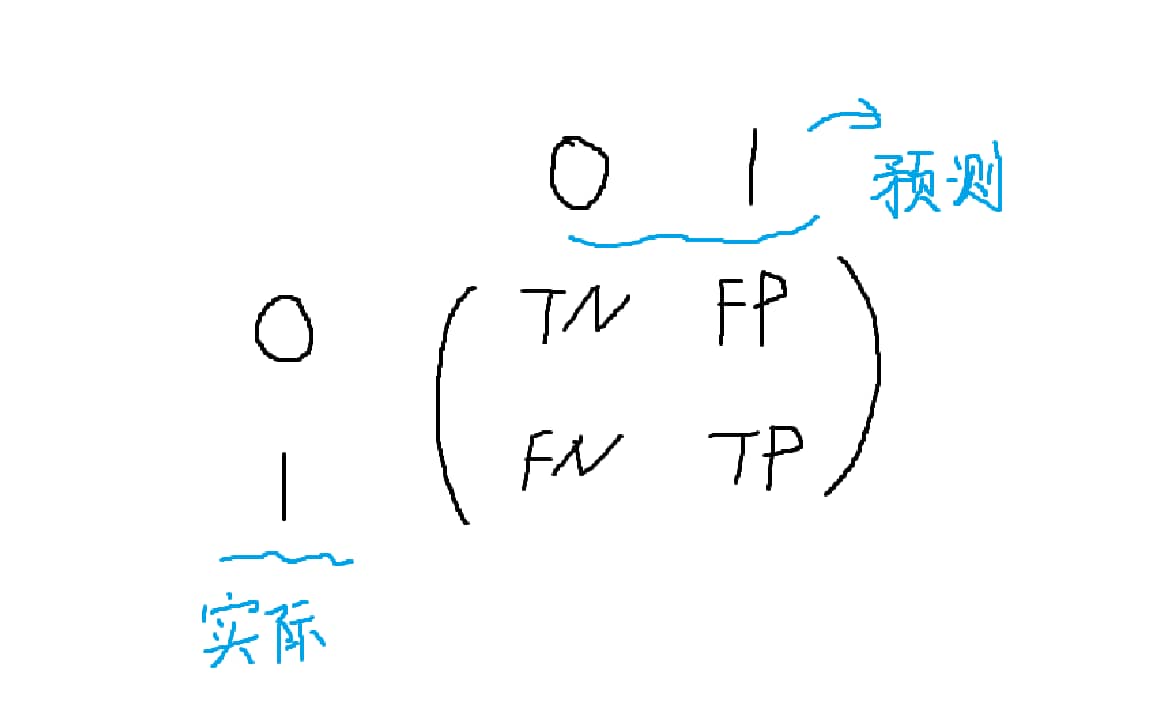
- 举例:
1 | from sklearn.metrics import confusion_matrix |
结果显而易见:
- TN: 2
- FP: 1
- FN: 2
- TP: 3
多分类混淆矩阵举例

结果如下所示:
1 | 0 1 2 |
混淆矩阵性能分析指标
二分类
- 准确率(Accuracy)
- 目的:衡量模型整体预测正确的比例
- 精确率(Precision)
- 目的:求预测为正例的样本中,有多少是真正的正例(减少假阳性,即减少误报)
- 例子:垃圾邮件分类中,“预测为垃圾的邮件里,有多少真是垃圾?”
- 召回率(Recall,灵敏度)
- 目的:求真实正例中,有多少被正确预测(减少假阴性,即减少漏报)
- 例子:疾病检测中,“所有真实患病的人里,有多少被检测出来了?”
- F1-Score
- 目的:由于高精确率可能伴随低召回率(如模型只对极确信的样本预测为正例,漏掉许多真实正例)。而高召回率可能伴随低精确率(如模型激进预测,导致大量误报)。我们需要一个东西来中和,即进行精确率和召回率的调和平均
多分类
- 由于多分类存在多个类别,每个类别都需要单独评估,存在多个类别(如类别A、B、C…),每个类别都需要单独评估,需要扩展计算方式以涵盖所有类别的交互情况。
- 针对多分类,我们可以采用Micro或Macro。Micro和Macro是两种不同的聚合方式。
- Micro-Averaging(微平均)
- 方法:将所有类别的TP、FP、FN汇总后,再计算指标
1 | | | 预测A | 预测B | 预测C | |
- 精确率(Precision)
- 此时;FP同理
- 召回率(Recall,灵敏度)
- 此时;FN同理
- 举例

- 举例:
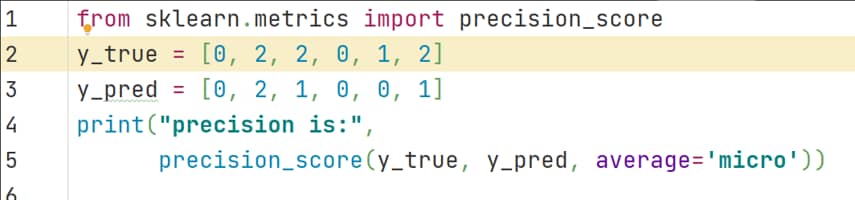
结果:precision_score is: 0.5
- Macro-Averaging(宏平均)
- 方法:先计算每个类别的Precision/Recall,再对所有类别取算术平均。

- 举例

结果:precision_score is: 0.22222222222
总结
- 若需减少误报(如垃圾邮件过滤),优先优化精确率。
- 若需减少漏报(如癌症筛查),优先优化召回率。
- 若需二者均衡,使用F1-Score。
分析模型错误类型
- FP(假阳性)过高:模型过于敏感,误判负例为正例。
- FN(假阴性)过高:模型过于保守,漏判正例。
分类器的评估方法
分类器的性能和所选的测试集和训练集有直接的关系,如果用训练集数据作测试集来测试分类器的性能,模型的准确度显然令人难以信服,我们可以通过不同方法划分测试集与训练集,用测试集评估分类器性能、
保持法
- 将给定的数据随机划分为两个独立的集合:训练集和测试集。通常1/3的数据作为训练集,2/3的数据作为测试集。
- 注意:相对于整体而言,训练数据集越多,所得到分类器的性能越好
交叉验证
- 将数据随机分为不相交的n份,每份大小相等,训练和测试都进行n次。从结果来看,最后可以得到n个不同的准确率,再求得平均准确率。
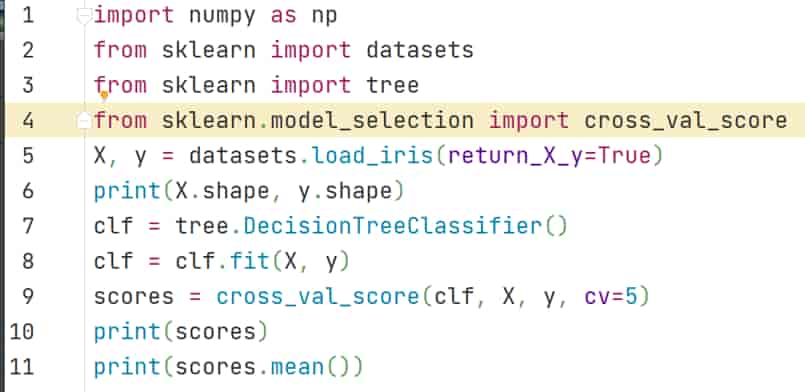
关联规则
频繁项目集生成算法
Apriori算法
定理
- 如果项目集X 是频繁项目集,那么它的所有非空子集都是频繁项目集。
- 如果项目集X 是非频繁项目集,那么它的所有超集都是非频繁项目集。
算法
1 | L_1 = {large 1-itemsets}; // 所有1-项频集 |
举例
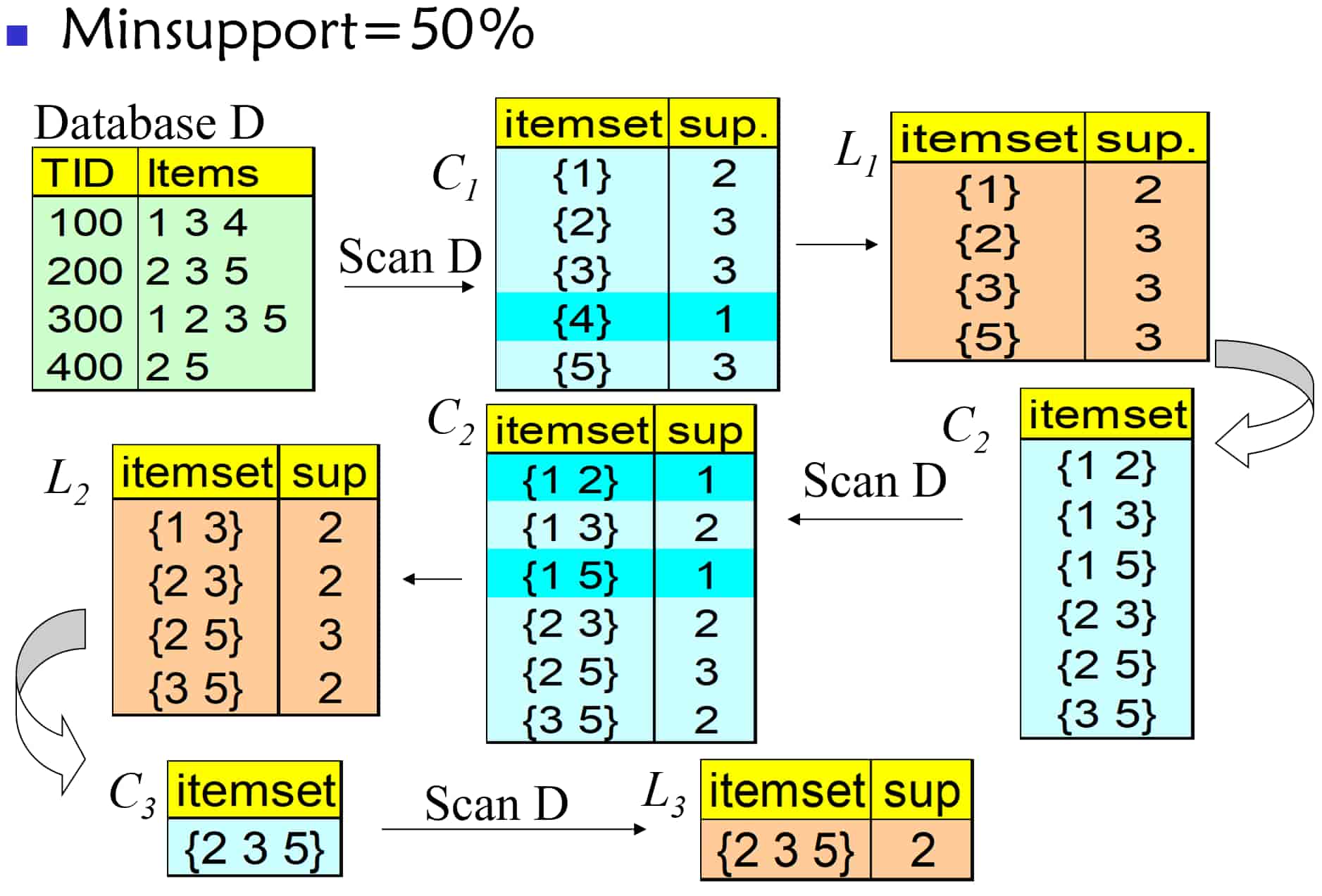
FP-tree算法
- 介绍:只进行两次数据库扫扫描(第一次扫描数据库获取频繁1项集,第二次扫描建立FP-tree树。),不使用候选集,直接压缩数据库成一个频繁模式树,最后通过FP-growth挖掘频繁项集。同种操作的Apriori算法 在产生频繁模式完全集前需要对数据库进行多次扫描,同时产生大量的候选频繁集,这就使Apriori算法时间和空间复杂度较大。FP-tree首先利用事务数据库中数据构造FP-tree,再通过FP-tree挖掘频繁模式。
构造FP-tree
- 第一次扫描数据库,生成1频繁项集L1,生成的L1根据support按降序排列。
- 第二次扫描建立FP-tree(简称T),对每条事务中的项进行过滤和排序,即通过去掉不频繁单项目简化原始项目集,生成整理后项目集N,整理后的项目集已经删去了单项目非频繁项目集。将N的每一条事务根据L的顺序重新排列。在对每一条事务排序的同时,事务中的每一项添加到T中,逐步生成完整的FP-tree。

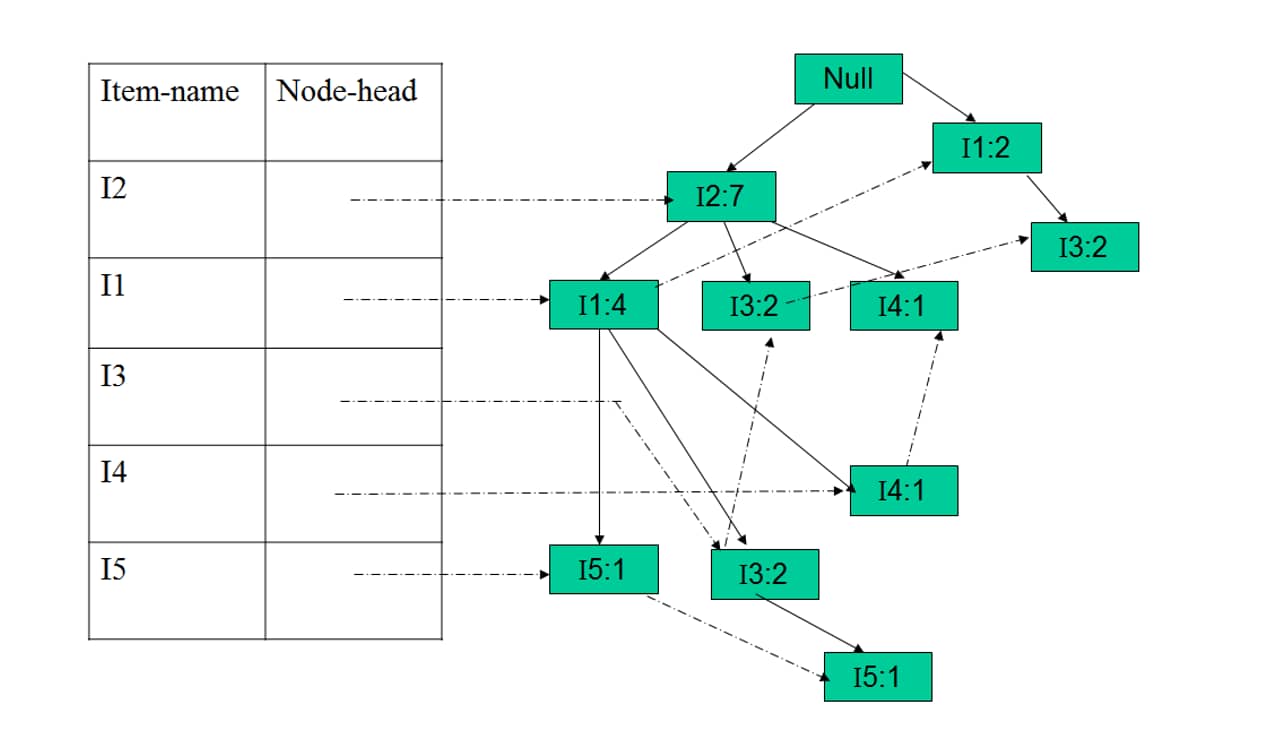
- 通过图2我们可以清楚的看出在FP-tree中,L通过顺序表做Header-Table,每条事务中的项作节点构成了一颗树,同时相同的项之间显示构成链表。
从FP-tree中挖掘频繁模式
- 综述:采用分治的基本思想,对于每个项,生成它的条件模式基,再根据条件模式基生成条件模式树,对于每个新生成的条件模式树,重复这个步骤,直至FP-tree为空,或只含唯一的一个路径(此路径的每个子路径对应的项目集都是频繁项目集)
- 将L1按照倒序开始遍历
- 对L1中每个遍历的项目生成它的条件模式基
- 根据条件模式基生成对应的条件模式树(根据minisupport)
- 重复这一过程并产生相应的频繁模式
后续操作
- 整理所有的频繁模式,找出最大频繁模式
- 用BFS或DFS算法求解对应的强关联规则
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 智码Moss!
评论








